Question

Seatwork # Find the measure of the angle indicated in bold.

Answer 1

Before we start we need to remember that co-interior angles are supplementary, that is, they add up to 180°.

First diagram.

The angles shown are co-interior angles, then we have:

`\begin{gathered} x+96+x+96=180 \\ 2x+192=180 \\ 2x=180-192 \\ 2x=-12 \\ x=-(12)/(2) \\ x=-6 \end{gathered}`

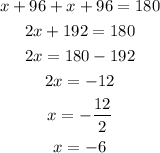
Once we have the value of x we plug it in the expression of the angle we want to know to find it:

`-9+96=90`

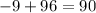
Therefore, the angle is 90°.

Second diagram.

Once again the angles shown are co-interior then we have:

`\begin{gathered} x+109+x+89=180 \\ 2x+198=180 \\ 2x=180-198 \\ 2x=-18 \\ x=-(18)/(2) \\ x=-9 \end{gathered}`

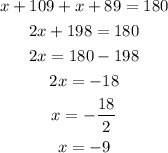
Plugging the value of x in the expression for the bolded diagram we have:

`-9+89=80`

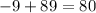
Therefore, the angle in the second diagram is 80°