Question

A toy manufacturer needs a piece of plastic in the shape of a right triangle with one leg 4 cm longer than the other and the hypotenuse 8 cm longer than the shorterleg. What is the perimeter of the triangle?The perimeter is ___(Simplify your answer.)

Answer 1

Given

It is given that the longer leg is 4 cm longer than the shorter leg.

It is also given that the hypotenuse is 8 cm longer than the shorter leg.

Step-by-step explanation

Let the shorter leg be x.

The longer leg be y.

Then the relation formed is

`y=x+4`

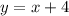
It is also given that the hypotenuse is 8 cm longer than the shorter leg.

Let the hypotenuse is z.

`z=8+x`

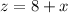
Then the perimeter of the right triangle is the sum of all the sides.

`x+y+z`

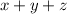
But to find the value of x , use the Pythagoras theorem.

`z^2=y^2+x^2`

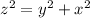
Substitute the values.

`\begin{gathered} (8+x)^2=(4+x)^2+x^2 \\ 64+x^2+16x=16+x^2+8x+x^2 \\ 64+16x=16+8x+x^2 \\ 64-16+16x-8x-x^2=0 \\ -x^2+8x+48=0 \end{gathered}`

Solve the quadratic equation to find the value of x.

`\begin{gathered} (x-12)(x+4)=0 \\ x=12,-4 \end{gathered}`

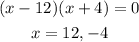
As x cannot be negative , then the value of x is 12.

The length of shorter leg is 12.

The length of longer leg is 12+4=16.

The hypotenuse is 12+8=20.

Now , the perimeter of right triangle is

`\begin{gathered} P=12+16+20 \\ P=48cm \end{gathered}`

Answer

The perimeter of the triangle is 48 cm.