Question

Solve the following system of equations.5x + 6y = 04x5y =49Px =

Answer 1

`x=-6, y=5`

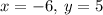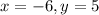
1) Let's solve this system of equations, by using the Elimination Method so, let's begin by multiplying by (-4) and (5) respectively so we can eliminate the x-terms when adding both equations simultaneously:

`\begin{gathered} 5x+6y=0 \\ 4x-5y=-49 \\ \\ 5x+6y=0\:*(-4) \\ 4x-5y=-49\:*(5) \\ \\ -20x-24y=0 \\ 20x-25y=-245 \\ --------- \\ -49y=-245 \\ \\ (-49y)/(-49)=(-245)/(-49) \\ \\ y=5 \end{gathered}`

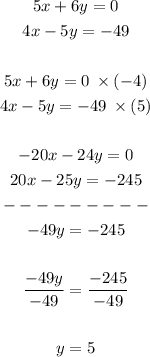
2) Now, let's plug y=5 into any original equation to solve for x:

`\begin{gathered} 5x+6(5)=0 \\ \\ 5x+30=0 \\ \\ 5x+30-30=-30 \\ \\ 5x=-30 \\ \\ (5x)/(5)=-(30)/(5) \\ \\ x=-6 \end{gathered}`

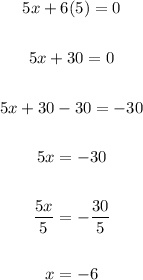
3) Hence, the answer is:

`x=-6,\:y=5`