Question

1. Consider the function.a) Algebraically find the zeros and their multiplicities for this function.

Answer 1

x = -1, x = -1, x = 1;

-1 has a multiciplicity of 2

+1 has a multiciplicity of 1

Step-by-step explanation

We have the function:

`f(x)=x^3+x^2-\text{ x - 1}`

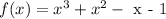
To find the zeros of the function, we have to make the function = 0.

That is:

`x^3+x^2\text{ - x - 1 = 0}`

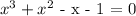
Now, factorise the function:

`\begin{gathered} \Rightarrow x^2(x\text{ + 1) - 1(x + 1) = 0} \\ \Rightarrow(x^2\text{ - 1)(x + 1) = 0} \\ Factorise(x^2\text{ - 1):} \\ (x\text{ + 1)(x - 1)}(x\text{ + 1) = 0} \\ \Rightarrow\text{ x = -1, x = 1 and x = -1} \end{gathered}`

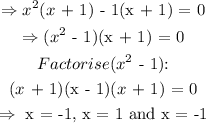
Those are the zeros of the function.

The multiciplicities of this function simply refer to the number of times a certain root (or zero) of the function appears in the function.

Therefore:

-1 has a multiciplicity of 2 (it appears twice)

+1 has a multiciplicity of 1