Question

I don’t know the answer I can’t find any pattern

Answer 1

The given sequence is:

`9,-18,27,-36,\ldots`

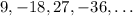
It is required to find the nth term of the sequence as suggested by the pattern.

Rewrite the terms of the sequence as follows:

The powers can be written as:

`9*(-1)^(1+1)*1,9*(-1)^(2+1)*2,9*(-1)^((3+1))*3,9*(-1)^((4+1))*4,\ldots`

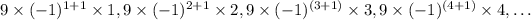
From the pattern above, it follows that the nth term of the sequence is:

`\begin{gathered} \lbrace a_n\rbrace=\lbrace9*(-1)^(n+1)* n\rbrace \\ \Rightarrow\lbrace a_n\rbrace=\lbrace(-1)^((n+1))\cdot9n\rbrace \end{gathered}`

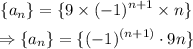
The nth term of the sequence is shown above.