Question

i have a question in Trig about tires spinning, angular speed, and revolutions per minute. Pic included

Answer 1

Step-by-step explanation

First of all, let's follow the suggestion given by the question and convert the speed of the truck from mi/h to in/min. We know that 1 mile is equivalent to 63360 inches and 1 hour is equivalent to 60 minutes. Then 55 mi/h is equivalent to:

`55\text{ }(mi)/(h)=55\text{ }(63360in)/(60min)=55\cdot(63360)/(60)(in)/(min)=58080(in)/(min)`

So we know that the truck travels 58080 inches in a minute. If we divide this distance by the circumference of the wheels we'll find the number of revolutions performed by them in a minute. The wheels have a 30 in diameter and since the circumference of a circle is given by the product between π and its diameter we have that the circumference of the wheels is:

`\pi\cdot30in=30\pi in`

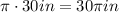
Then the number of revolutions performed by each wheel in a minute is:

`(58080)/(30\pi)=1936\pi`

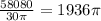
These are the rpm asked in the second question. This result can be used to solve the first part since we know that a revolution is performed when the wheels rotate 2π radians. This means that if we multiply the rpm by 2π we'll find the angular speed of the wheels in rad/min:

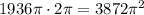
`1936\pi\cdot2\pi=3872\pi^2`Answer

Now that we found the quantities requested we should express them as decimal numbers rounded to 1 decimal place.

The first answer is: 38215.1 rad/min

The second answer is 6082.1 rpm