Step-by-step explanation
To find the surface area of the pyramid, we will find the area of the square base and sum it to the areas of the triangular surfaces.
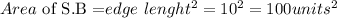
The area of one triangular surface is
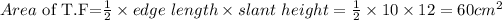
Since the triangular prism has four triangular surfaces, therefore the sum of the area of the triangular faces is
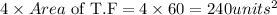
Therefore, the surface area of the triangular prism becomes
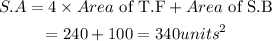
Answer: Option A