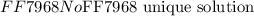Question

Y = 2x - 3- 6x + 3y = -9In substitution form

Answer 1

We will investigate how to solve simultaneous equations using "substitution method".

The substitution method is a step-wise approach as follows.

Step 1: Express any of the equation as an explicit equation between two variables

In this step we will choose either one of the equation and then we choose any one variable from the chosen equation that we want isolate. Then algebraically manipulate the equation and isolate the chosen variable ( isolating it to one side of the " = " sign ). Then express the chosen variable in terms of the other variable as follows:

`y\text{ = 2x - 3 }\ldots\text{ Eq1}`

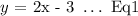
Step 2: Substitute the expression developed above in the other equation.

The second equation given to us in the problem is:

`-6x\text{ + 3y = -9 }\ldots\text{ Eq2}`

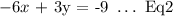
We will substitute the equation developed in the previous step and plug it in the Eq2 as follows:

`-6x\text{ + 3}\cdot(\text{ 2x - 3 ) = -9}`

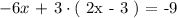
Step 3: Solve for the non-chosen variable

Once we substituted our expression in the other equation we were left with a single variable equation which is solvable by algebraic manipulation as follows:

`\begin{gathered} -6x\text{ + 6x -9 = -9} \\ \textcolor{#FF7968}{-9}\text{\textcolor{#FF7968}{ = -9}} \end{gathered}`

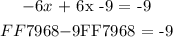
Unfortunately, the variable got cancelled out during algebraic manipulation. Such equations are called " dependent " equations. This means that we can obtain Eq2 from Eq1 OR Eq1 and Eq2 by multiplying/dividing either equation with a constant to obtain the other equation.

`\begin{gathered} 3\cdot\textcolor{#FF7968}{Eq1} \\ 3\cdot\text{ ( y = 2x - 3 )} \\ 3y\text{ = 6x - 9} \\ \textcolor{#FF7968}{3y}\text{\textcolor{#FF7968}{ - 6x = -9 }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq2}} \end{gathered}`

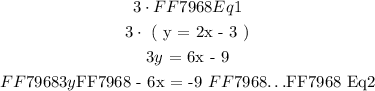
Dependent equations do not have a unique solution. They have multiple solution because we have 1 equation and 2 variable. We have to given arbitrary values to either variable and then we can solve for the other variable. However, the solved solution depends on the supposed value of the variable.

Hence,

`\textcolor{#FF7968}{No}\text{\textcolor{#FF7968}{ unique solution}}`