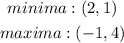Question

Find the absolute extrema of the function on the closed interval.f(x) = 3 − x, [−1, 2]minimum (x, y) = maximum (x, y) =

Answer 1

Given:

There are given the function:

`f(x)=3-x`

Step-by-step explanation:

To find the maxima and minima extrema, first, we need to find the difference between the given function:

So,

`\begin{gathered} f(x)=3-x \\ f^(\prime)(x)=-1 \end{gathered}`

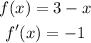
Now,

Since f'(x) exists for all x, the only critical numbers of occure when f'(x) = 0.

Then,

According to the given differentiation, there are no critical points.

That means:

`-1\\e0`

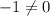
Now,

The values at the endpoints of the interval, put -1 and 2 into the above function:

`f(-1)=4`

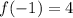
And,

`\begin{gathered} f(x)=3-x \\ f(2)=3-2 \\ f(2)=1 \end{gathered}`

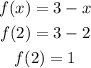
Comparing these two numbers, we see the absolute maximum value and the absolute minimum values.

Final answer:

Hence, the minimum and maximum extrema are shown below:

`\begin{gathered} minima:(2,1) \\ maxima:(-1,4) \end{gathered}`