Question

Circle X is shown with inscribed triangle ABC, B В A 40° X 'C с Part A. Find mzc. Part B. Find the measure of arc BC. Part A

Answer 1

As AC is the diameter of the circle, the measument of angle B will be 90 degrees.

The measurement of angle C can be determined as,

`\begin{gathered} \angle A+\angle B+\angle C=180^(\circ) \\ 40^(\circ)+90^(\circ)+\angle C=180^(\circ) \\ \angle C=50^(\circ) \end{gathered}`

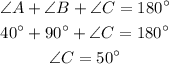
Thus, measure of angle C is 50 degrees.

The measure of arc BC can be determined as,

`\begin{gathered} \text{mBC}=2*40^(\circ) \\ =80^(\circ) \end{gathered}`

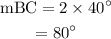
Thus, arc BC subtends 80 degrees at the center.