Question

the Nelson family and the Roberts family each used their sprinklers last summer water output rate for the Nelson family sprinkler was 15 liters per hour the water output rate for the Roberts family sprinkler was 20 liters per hour. The families used their sprinklers for a combined total of 50 hours resulting in a total water output of 900 how long was each sprinkler used

Answer 1

Let N be the time that the Nelson family used their sprinkler, and R be the time that the Roberts family used it, both measured in hours.

The total amount of time that sprinkers were used is N+R, which is equal to 50 hours according to the text.

Since the rate of the Nelson family's sprinkler is 15 liters per hour, then they used a total of 15N liters. From a similar reasoning, the total amount of water used by the Roberts family is 24R. The total water output is then 15N+24R, which is equal to 900.

Then, we have a 2x2 system of equations:

`\begin{gathered} N+R=50 \\ 15N+20R=900 \end{gathered}`

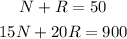
Multiply both sides of the first equation by 15:

`\begin{gathered} N+R=50 \\ \Rightarrow15(N+R)=15(50) \\ \Rightarrow15N+15R=750 \end{gathered}`

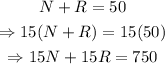
Then, the system is equivalent to:

`\begin{gathered} 15N+15R=750 \\ 15N+20R=900 \end{gathered}`

Substract the first equation of the system from the second one:

`\begin{gathered} (15N+20R)-(15N+15R)=900-750 \\ \Rightarrow15N+20R-15N-15R=150 \\ \Rightarrow5R=150 \\ \Rightarrow R=(150)/(5) \\ \Rightarrow R=30 \end{gathered}`

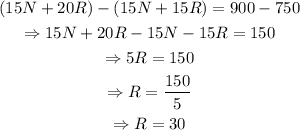
Plug in R=30 into the first equation to find N:

`\begin{gathered} N+R=50 \\ \Rightarrow N+30=50 \\ \Rightarrow N=50-30 \\ \Rightarrow N=20 \end{gathered}`

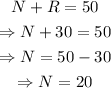
Therefore, the Nelson family's sprinkler was used for 20 hours and the Robert family's sprinkler was used for 30 hours.