Question

Two identical hockey pucks collide. Puck A is initially moving to the right at 5 m / s when it collides with puck B. After the collision, puck A moves at 2.0m / s at an angle of 30 degrees from its original direction. What is the speed and direction of puck B after the collision? Is this an elastic collision?

Answer 1

Given:

• Initial velocity of Puck A, u1 = 5 m/s

,

• Final velocity of Puck A, v1 = 2.0 m/s

,

• θ = 30 degrees

,

• Initial velocity of puck B = 0 m/s

Let's find the speed and direction of puck B after the collision.

Apply the Law of Conservation of momentum:

`p_(1A)+p_(1B)=p_(2A)+p_(2B)`

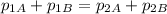
Thus, we have:

`m_Au_A+m_Bu_B=m_Av_A+m_Bv_B`

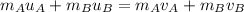
Since the two Pucks are identical, this means they have the same masses.

Now, we have the x- and y-components

`\begin{gathered} x-component: \\ p_(1A)cos30+p_(2A)cos60=p_(1B)+0 \\ \\ y-component: \\ p_(1A)sin30-p_(2A)sin60=0+0 \\ p_(1A)sin30=p_(2A)sin60 \\ p_(1A)=(p_(2A)sin60)/(sin30) \end{gathered}`

`\begin{gathered} p_(1B)=(p_(2A)sin60)/(sin30)cos30+p_(2A)cos60 \\ \\ p_(1B)=p_(2A)((sin60)/(sin30)cos30)+cos60) \end{gathered}`

`.`

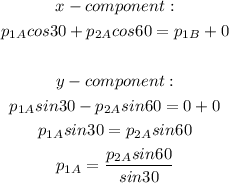
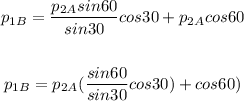
Now, to find the speed of puck B after collision, we have:

`\begin{gathered} v_(2B)=\sqrt{(v_(AB)cos\theta_1-u_A)^2+(v_Asin\theta)^2} \\ \\ v_(2B)=√((2.0cos30-5)^2+(2.0sin30)^2) \\ \\ v_(2B)=3.42\text{ m/s} \end{gathered}`

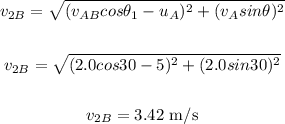
The speed of puck B after the collision is 3.42 m/s.

Since the puck has a speed after collision, this is an elastic collision.

To find the direction, we have:

`\begin{gathered} \theta_1-\theta_2=90 \\ \\ \theta_2=\theta_1-90=30-90=-60^o \end{gathered}`

Therefore, the direction is 60 degrees in the opposite direction.

ANSWER:

Speed of puck B after the collision = 3.42 m/s

Direction = 60 degrees in the opposite direction.