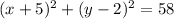Question:
Solution:
An equation in the standard form of the circle with center (h,k) and radius r is given by the following formula:

a)
Consider the following circle equation:
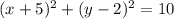
According to the standard form equation for a circle, we can conclude:
Center of the circle = (-5, 2)
The radius of the circle = √10
b) According to the standard form equation for a circle, we have that a circle with center (-5, 2 ) will have the following provisional equation:
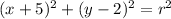
to find r, we can use the coordinates of the point (x,y)=(2,-1) into the above equation and solve for r:
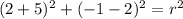
this is equivalent to:
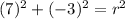
this is equivalent to:
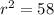
solving for r, we obtain:
![r=\sqrt[]{58}](https://img.qammunity.org/2023/formulas/mathematics/college/lkei2c2doyrwhwi1muet10qpcxdcahxcnl.png)
so that, we can conclude that the equation of the circle would be: