Question

The revenue for selling x units of a product is R = 40x. The cost of producing x units is C = 20x+10500. In order to obtain a profit, the revenue must be greater than the cost, so we want to know, for what values of x will this product return a profit.To obtain a profit, the number of units must be greater than _____

Answer 1

the number of units must be greater than 525

Step-by-step explanation:

Revenue for selling x units is R = 40x

The cost for producing one unit of the x is C = 20x + 10500

To obtain profit, revenue > cost

To determine the number of x that will be produced to return a profit, we need to find break even point

At break-even point, cost = revenue

`\begin{gathered} C=R \\ 40x\text{ = 20x + 10500} \\ subtract\text{ 20x from both sides:} \\ 40x\text{ - 20x = 10500} \\ 20x\text{ = 10500} \end{gathered}`
`\begin{gathered} divide\text{ both sides by 20:} \\ (20x)/(20)\text{ = }(10500)/(20) \\ x\text{ = 525} \end{gathered}`

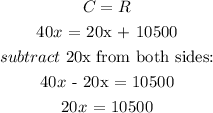
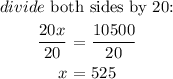
when x = 525, there is no profit as the value of cost is the same as the value of revenue.

For the products to return a profit, the number of x units produced will be greater than 525.

To obtain a profit, the number of units must be greater than 525