Question

I need 2 points to the left of vertex, I need the vertex, and I need 2 points to the right of the vertex. please quickly i am timed

Answer 1

Step-by-step explanation:

Given the below quadratic equation in vertex form;

`y=(x+4)^2-2`

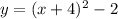
Recall that a quadratic equation in vertex form is generally given as;

`y=(x-h)^2+k`

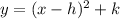
where (h, k) is the vertex of the parabola

If we compare both equations, we can see that h = -4 and k = -2, therefore the vertex of the given parabola is (-4, -2).

To determine two points to the left of the vertex, we'll choose x = -5 and x = -7.

When x = -5, let's find y;

`\begin{gathered} y=(-5+4)^2-2 \\ =(-1)^2-2 \\ =1-2 \\ =-1 \end{gathered}`

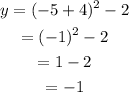
When x = -7, let's find y;

`\begin{gathered} y=(-7+4)^2-2 \\ =(-3)^2-2 \\ =9-2 \\ =7 \end{gathered}`

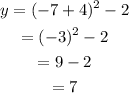
To determine two points to the left of the vertex, we'll choose x = -3 and x = -1.

When x = -3, let's determine the value of y;

`\begin{gathered} y=(-3+4)^2-2 \\ y=(1)^2-2 \\ y=1-2 \\ y=-1 \end{gathered}`

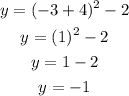
When x = -1, let's determine the corresponding value of y;

`\begin{gathered} y=(-1+4)^2-2 \\ y=(3)^2-2 \\ y=9-2 \\ y=7 \end{gathered}`

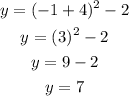
With the above points, we can go ahead and graph the parabola as seen below;