Question

A rock is thrown upward with a velocity of 18 meters per seconds from the top of a 37 meters high Cliff, and it Misses the Clift on the way back down. When will the rock be at 2 meters from ground level? Round your answer to two decimal places

Answer 1

5.08 seconds after being thrown

Step-by-step explanation

Given:

• The initial vertical velocity of the rock, u = 18 m/s

,

• The initial height of the rock, y₀ = 37 m

Find:

• The time it takes the rock to be at 2 m from ground level, t

The vertical displacement of an object is given by,

`y=y_o+ut-(1)/(2)gt^2`

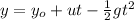
Where g is the acceleration of gravity, 9.8 m/s².

So, in this case, the height of the rock is given by the equation,

`y=37+18t-4.9t^2`

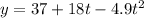
We have to find for what value of t, y = 2,

`37+18t-4.9t^2=2`

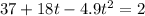
Subtract 2 from both sides,

`\begin{gathered} 37-2+18t-4.9t^2=2-2 \\ \\ 35+18t-4.9t^2=0 \end{gathered}`

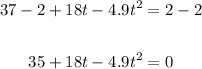
To solve this equation, we can use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ \\ x=(-b\pm√(b^2-4ac))/(2a) \end{gathered}`

In this case, a = -4.9, b = 18, and c = 35,

`t=(-18\pm√(18^2-4\cdot(-4.9)\cdot35))/(2\cdot(-4.9))=(-18\pm√(324+686))/(-9.8)=(-18\pm√(1010))/(-9.8)\approx(-18\pm31.78)/(-9.8)`

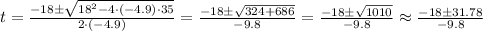
The two possible solutions are,

`\begin{gathered} t_1=(-18-31.78)/(-9.8)=(-49.78)/(-9.8)\approx5.08 \\ \\ t_2=(-18+31.78)/(-9.8)=(13.78)/(-9.8)\approx-1.41 \end{gathered}`

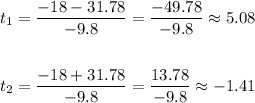
Of these two results, t₂ is inconsistent with the problem. Remember that t represents time, so it cannot be negative.

Hence, we can conclude that the rock will be at 2 m from ground level 5.08 seconds after being thrown.