Question

A committee of 4 is being formed randomly from the employees at a school: 4 administrators, 32 teachers, and 5 staff. What is the probability that all 4 members are teachers? Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.

Answer 1

We have to find the probability that the commitee of 4 is being formed by the 4 teachers.

We have 32 teachers from a total of 4+32+5 = 41 employees.

We can calculate the probability in steps:

1) We find the probability that a teacher is chosen for the first place in the commitee. In this case, the order does not matter, but we use the places as a way to express the steps.

We can calculate this probability as 32/41, as we have 32 teachers out of 41 employees.

2) Now, we calculate the probability that a teacher is chosen for the second place. As one teacher has been already selected, we are left with 31 teachers out of 40 employees.

Then, the probability is 31/40.

3) In the same way, for the third place, we have the probability that a teacher is chosen as 30/39.

4) For the fourth place the probability is 29/38.

We can then write the probability that all four places are occupied by teachers by multiplying this 4 probabilities:

`\begin{gathered} P(\text{TTTT})=P(x_1=T)\cdot P(x_2=T)\cdot P(x_3=T)\cdot P(x_4=T) \\ P(\text{TTTT})=(32)/(41)\cdot(31)/(40)\cdot(30)/(39)\cdot(29)/(38) \\ P(\text{TTTT})=(863040)/(2430480) \end{gathered}`

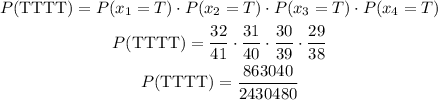
We can easily simplify this fraction using the fractions we already have and grouping them as:

`\begin{gathered} P=(32)/(41)\cdot(31)/(40)\cdot(30)/(39)\cdot(29)/(38) \\ P=(2^5)/(41)\cdot(31)/(2^3\cdot5)\cdot(3\cdot2\cdot5)/(3\cdot13)\cdot(29)/(2\cdot19) \\ P=(2^6\cdot3\cdot5\cdot29\cdot31)/(2^4\cdot3\cdot5\cdot13\cdot19\cdot41) \\ P=(2^2\cdot29\cdot31)/(13\cdot19\cdot41) \\ P=(3596)/(10127) \end{gathered}`

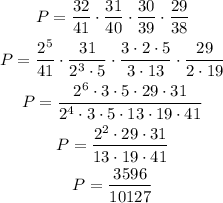
Answer: the probability is 3596/10127 or 0.355090.