The 5th term and 8th term of a geometric sequence are given to be 10 and 80, respectively.
It is required to find the first term and the common ratio.
Recall the Explicit Formula for a geometric sequence:
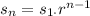
Substitute n=5 into the formula:
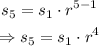
Substitute s₅=10 into the equation:
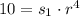
Use the same procedure for s₈ to get the second equation:
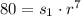
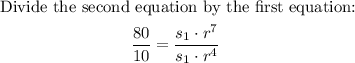
Simplify the equation and solve for r:
![\begin{gathered} 8=r^(7-4) \\ \Rightarrow8=r^3 \\ \Rightarrow r=\sqrt[3]{8}=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ch9nr5eekkjk0mp4dhsia04z142eeq92oz.png)
Substitute r=2 into the first equation:
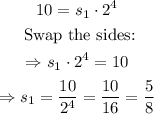
Answers:
s₁=5/8, r=2
T