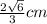Question

2. SABC is a regular triangular pyramid with all sides equal to 2 cm. Calculate the pyramid: 1) the length of the apothem; 2) the length of the apex.

Answer 1

Given:

SABC is a regular triangular pyramid with all sides equal to 2 cm.

That is,

`s=2cm`

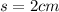
To find:

1) The length of the apothem.

2) The length of the apex.

Step-by-step explanation:

1)

Since it is a regular triangular pyramid.

So, it has 3 equilateral triangular faces.

The apothem "a" formula is given by,

`a=(s)/(2√(3))`

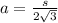
Substituting the side length, we get

`\begin{gathered} OM=(2)/(2√(3)) \\ OM=(1)/(√(3))cm \end{gathered}`

2)

Here, the slant height is,

`l=2cm`

The length of the apothem is,

`a=OM=(1)/(√(3))cm`

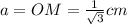
By Pythagoras theorem,

`\begin{gathered} SC^2=MC^2+SM^2 \\ 2^2=((2)/(2))^2+SM^2 \\ 4=1+SM^2 \\ SM^2=3 \\ SM=√(3)cm \end{gathered}`

Next, we find the length of the apex from O.

That is the length of SO.

Using the Pythagoras theorem,

`\begin{gathered} SM^2=OM^2+SO^2 \\ (√(3))^2=((1)/(√(3)))^2+SO^2 \\ 3=(1)/(3)+SO^2 \\ SO^2=3-(1)/(3) \\ SO^2=(8)/(3) \\ SO=\sqrt{(8)/(3)} \\ =(2√(2))/(√(3)) \\ =(2√(2))/(√(3))*(√(3))/(√(3)) \\ SO=(2√(6))/(3)cm \end{gathered}`

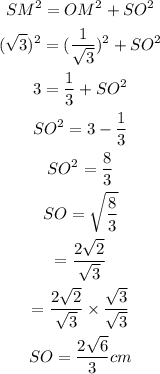
Therefore, the length of the apex is,

`(2√(6))/(3)cm`

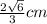
Final answer:

The length of the apothem is,

`a=OM=(1)/(√(3))cm`

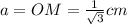
The length of the apex is,

`(2√(6))/(3)cm`