Question

Which set of numbers does not represent the length of the sides of a triangle

Answer 1

To find which set of numbers that do not represent the length of the sides of a triangle, we must apply the triangle inequality theorem.

The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

The conditions are:

`\begin{gathered} a+b>c \\ b+c>a \\ a+c>b \\ \text{where the set of lengths of sides are in the form }\mleft\lbrace a,b,c\mright\rbrace \end{gathered}`

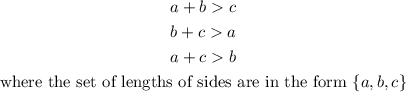
For option 1 : {9,12,19}

`\begin{gathered} 9+12>19 \\ 12+19>9 \\ 9+19>12 \\ \text{Hence option 1 represents the length of the sides of a triangle} \end{gathered}`

For option 2:{6,8,11}

`\begin{gathered} 6+8>11_{} \\ 8+11>6 \\ 6+11>8 \\ \text{Hence option 2 represents the length of the sides of a triangle} \end{gathered}`

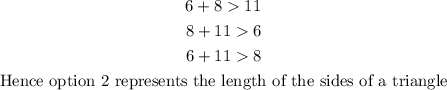
For option 3:{7,18,11}

`\begin{gathered} 7+8>11 \\ 18+11>7 \\ 7+11\text{ is not > 18} \end{gathered}`

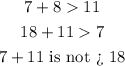
Hence option 3 does not represent the length of the sides of a triangle since sum of the length of two sides ia not greater than the length of the third side

The answer is therefore : {7,18,11}