Notice that the parallelogram has 2 equal sides and one right angle, therefore, the parallelogram is a square.
Then, we have that the diagonals are perpendicular, which gives us the following equation:
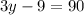
solving for y we get:

we also have that each diagonal bisect the angles of the square. Since all the angles are right angles, we have for x and z:
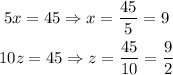
therefore, y = 33, x = 9 and z = 9/2