To solve this problem, we have to multiply the possible number in each digit.
So, the thousand's place has 9 options because zero can take this place. The hundred's place has 9 options too because we already used a digit on thousand's place. Then, there are 8 options for ten's place, and at last, there are 7 options for unit's place.
Now, we just have to multiply
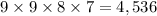
Hence, the are 4,536 possible 4-digit numbers.