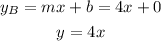First, we have to get the slope ( m ) of the Line a based on the two points given:
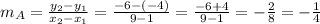
As they are perpendicular lines, the slope of Line a is the inverse of the slope of Line b with different sign. Therefore...
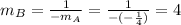
Finally, we find the constant of the equation using the point given of Line b.

Answer: