We have an initial mass of 3 grams.
This element has a half life of 1620 years.
We have to calculate the remaining mass after 4500 years.
We first define the model for the remaining mass in function of time.
The model is:
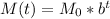
The initial mass M0 is 3 grams.
We can find the expression for b knowing that the half life is 1620. This means that the mass at time (t+1620) will be half the mass at time t:
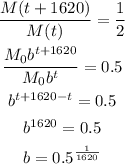
We then have the model as:
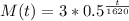
We can then use thiis model to calcualte the mass for t = 4500:
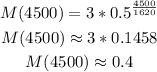
Answer: the mass after 4500 years is approximately 0.4 grams.