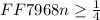Question

21) 10 - 4 1 - 811 56 -7 -6 -5 -3 -2 -1 0 1 2 3 4 5

Answer 1

We are asked to solve the inequality

`10-4|1-8n|\leq6`

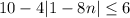
which can be decomposed into two separate inequalities

`10-4(1-8n)\leq6`

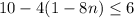
and

`10+4(1-8n)\leq6`

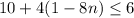
Let us solve the first inequality. by first subtracting 10 from both sides. Doing this gets us

`-4\mleft(1-8n\mright)\le-4`

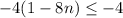
dividing both sides by -4 reverses the sign of the inequality; therefore, we get

`1-8n\ge1`

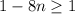
subtracting 1 from both sides gets us

`-8n>0`
`\textcolor{#FF7968}{\therefore n\leq0}`

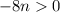
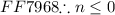
A similar process for the inequality 10 + 4(1-8n) ≤ 6 gives us the solution

`\textcolor{#FF7968}{n\ge(1)/(4)}`