Question

Question 54 what I’m suppose to do I’m not got is says evaluate

Answer 1

54. We need to find the value of the expression

`(1)/(12^(-1))`

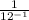
In order to do so, we can use the following definition for exponentials:

`\begin{gathered} x^(-1)=(1)/(x) \\ \\ (1)/(x^(-1))=\frac{1}{\frac{1}{x^{}}}=1\cdot(x)/(1)=x \end{gathered}`

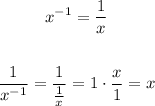
In this problem, we have x = 12. Thus, we can evaluate the expression as follows:

`(1)/(12^(-1))=12`

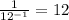
Let's see another way to find the same result.

Notice that when a number has the positive exponent n, it means that we have a product of n factors of that number. For example:

`\begin{gathered} 2^3=2\cdot2\cdot2=8 \\ \\ 2^1=2 \end{gathered}`

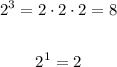
On the other hand, when the exponent is negative, by definition, the minus sign tells us to find the inverse of that number. For example:

`\begin{gathered} 2^(-3)=\mleft((1)/(2)\mright)^3=\mleft((1)/(2)\mright)\cdot\mleft((1)/(2)\mright)\cdot\mleft((1)/(2)\mright)\text{ because }(1)/(2)\text{ is the inverse of }2 \\ \\ 2^(-1)=(1)/(2) \end{gathered}`

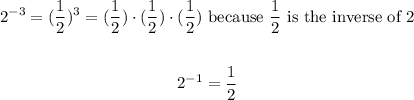
Also, notice that 1 to any exponent equals 1. For example:

`\begin{gathered} 1^0=1 \\ 1^1=1 \\ 1^2=1 \\ 1^(-1)=1 \end{gathered}`

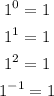
So, we can write:

`(1)/(12^(-1))=(1^(-1))/(12^(-1))=\mleft((1)/(12)\mright)^(-1)=\mleft((12)/(1)\mright)=12`

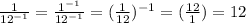
Therefore, the value of the given expression is 12.