We must solve graphically the following system of inequalities:
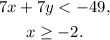
The question asks about the second linear inequality:
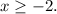
This inequality represents all the points with x-coordinate equal to or higher than -2. Plotting these points, we get the following graph:
From the graph we see that:
• The type of boundary line is ,solid (-), because the inequality has a ≥ sign,
,
• Two points of the boundary line are: ,(-2, 0),, ,(-2, 2),,
,
• the region that must be shaded is the region at the right,.
Answer
• Solid (-)
,
• (-2, 0), (-2, 2)
,
• the region that must be shaded is the region at the right.