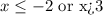The expressions we have are:
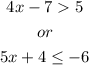
We need to solve each of these expressions, and since it is a compound inequality, the solution will be the solution of the first inequality OR the solution of the second inequality.
We start by solving:
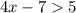
The first step is to add 7 to both sides:

The next step is to divide both sides by 4:
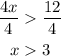
We have the first part of the solution: x>3
Now we need to solve the second inequality:
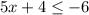
The first step is to subtract 4 to both sides:
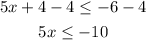
And the second step is to divide both sides by 5:
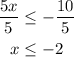
We have the second part of the solution. And since the initial conditions are one inequality OR the other, the same goes to express the solution:
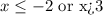
ANSWER: OPTION D