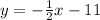Question

9. Three subway lines run along straight tracks in the city. The equation for each subway line is given. City planners want to add a fourth subway line and want the tracks for the four lines to form a rectangle. What is a possible equation for the fourth subway line? Justify your answer.

Answer 1

The general line equtaion passing through a point (x, y) is given by,

`y=mx+b`

Here, m is the slope and b is the y intercept.

The given equation can be written as,

`\begin{gathered} B\rightarrow y=2x+4 \\ N\rightarrow y=-(x)/(2)+4 \\ S\rightarrow y=2x-11 \end{gathered}`

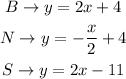
From the above equtaions, the slope for each line can be calculated as,

`\begin{gathered} B\rightarrow2 \\ N\rightarrow-(1)/(2) \\ S\rightarrow2 \end{gathered}`

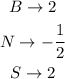
For two lines to be perpendicular, the slopes are reciprocal two each other and in opposite sign.

From the above equations we can say that, N is perpendicuar to B and S. For two parallel lines, the slopes are equal. Therefore we can say, B and S are parallel to ecah other.

Therefore, for the trcaks to form a rectangle, the fourth line should be made perpendicular to B and S and in parallel eith N.

Therefore, the slope of the line is, -1/2. Hence the possible equaton can be,

`y=-(1)/(2)x-11`