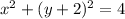The relation between cartesian coordinates (x, y) and polar coordinates (r, θ), is given by the following equations:

We must convert the following equation from polar coordinates to cartesian coordinates:
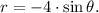
1) We multiply both sides of the equation by r:
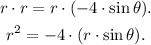
2) Now, we replace by the identities above:
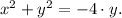
3) We rewrite the equation in the following way:
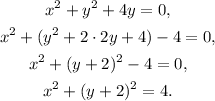
Answer
C.