Question

3. How many different 3-letter "words” can be made from the letters F,A,M,I,L,Y a. Repetitions are allowed?b. The first letter must be an f or m, and repetitions are allowed?c. No vowels can be used in the first and last spot, and repetitions are not allowed

Answer 1

Given:

The given letters are F, A, M, I, L, and Y.

So, there are 6 letters given.

Required:

We have to find the number of 3-letters "words" that can be made from the given letters when

(a) Repetitions are allowed.

(b) The first letter must be ab f or m, and repetitions are allowed.

(c) No vowels can be used in the first and last spot, and repetition is not allowed.

Step-by-step explanation:

Since all the letters are different so the number of permutations is

`^6P_3=120`

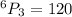
Number of 3-letters words that can be made from six given words

`\begin{gathered} =6*6*6 \\ =216. \end{gathered}`

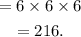
If the first letter will be f or m, then the number of 3-letters words that can be made from six given words

`\begin{gathered} =2*6*6 \\ =72. \end{gathered}`

If no vowels can be used in the first and last spot then the

number of 3-letters words that can be made from six given words