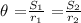Given that the angles of the two sectors are equal, we can find the relationship between the angles, radii, and the lengths of the arc
The length of the arc (S) is given by the formula
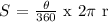
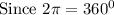
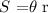
Then we can make the angle the subject of the formula
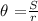
For the first sector
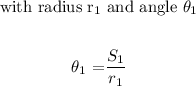
For the second sector
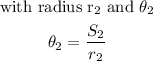
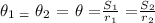
Simplifying the equation, we will obtain