different flavorsThe problem involves the use of permutation and combination equations to solve the number of ways to stack an ice cream cone with 4 scoops.
a. For the first case, we have six scoops available. The problem wants that each scoop must be different. Hence, we will use the permutation equation here to solve the problem.
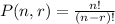
There are six available scoops, which means n = 6. The ice cream cone can only take 4 scoops, hence, r = 4. Substitute these in the equation above and solve, we get
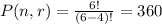
Hence, there can be 360 ways to stack an ice cream cone if each scoop is different.
b. For the second case, no restrictions are made on different flavors. This means that the flavor can be repeated in this scenario. If the limit of the scope in this problem is 4, and we have 6 different flavors. We have
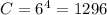
There are 1296 possible combinations that can be done if we don't have any restrictions on a different flavors.