Question

Find m,c show all the calculations that lead to the final answer

Answer 1

First, we have to find the length of arc AE, knowing that the arc BDA = 180°.

`\begin{gathered} arc(AE)=180-arc(BD)-arc(DE)=180-20-104 \\ \text{arc(AE)}=56 \end{gathered}`

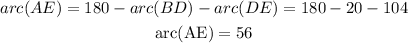
Then, we use the theorem about the angle formed by two secants, which is equivalent to the semi-sum of the difference between its subtended arcs.

`\begin{gathered} m\angle C=(1)/(2)(AE-BD)=(1)/(2)\cdot(56-20) \\ m\angle C=(1)/(2)\cdot36=18 \end{gathered}`

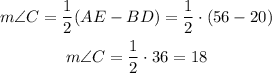
Therefore, angle C measures 18°.