Given r = -3 + 4 cos 0
To find the when r is maximum
We will find:
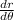
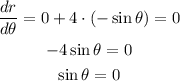
so, Theta = 0 or pi
So, when theta = 0
r = -3 + 4 cos 0 = -3 + 4 = 1
when theta = pi
r = -3 + 4 cos pi = -3 - 4 = -7
As r is the distance from the pole
So, the maximum distance occur at theta = pi
So, the answer is option d. π