Question

the sum of three numbers is 117. the third number is 4 times the second the furst number is 9 less than the second what are the numbers

Answer 1

We have three numbers that we will call x, y and z.

The sum of the three is 117, so we can write:

`x+y+z=117`

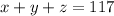
The third number, z, is 4 times the second (y). To write this in mathematical term we do:

`z=4\cdot y`

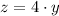
The first number, x, is 9 less than the second (y). Then, this is:

`x=y-9`

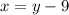
This is a system of linear equations with 3 unknowns and 3 equations.

We can use the two last equations to replace x and z in the first equation and find the value of y:

`\begin{gathered} x+y+z=117 \\ (y-9)+y+(4y)=117 \\ 6y-9=117 \\ 6y=117+9 \\ 6y=126 \\ y=(126)/(6) \\ y=21 \end{gathered}`

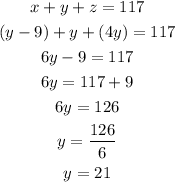
Now, with the value of y, we can calculate x and z:

`\begin{gathered} z=4y=4\cdot21=84 \\ x=y-9=21-9=12 \end{gathered}`

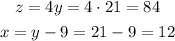
Answer: the numbers are 12, 21 and 84.