Given,
The function for the profit is,
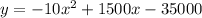
Differentiating the function with respect to x then,
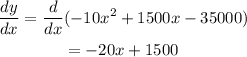
Check for maximum by second order differentiation,
Differentiating the function with respect to x then,
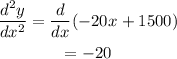
Negative sign shows the maximum.
For maximum, taking dy/dx=0 then,
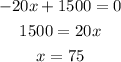
Subsituing the value of x in the function then,
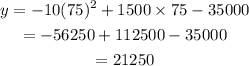
Hence, 75 admissions counselors should the college employ to maximize its profit.