According to the information given in the exercise:
- The empty tank is filled in 10 hours.
- The variable "x" represents the time (in hours) it takes pipe A to fill the tank and "y" represents the time (in hours) it takes pipe B to fill the tank.
- Pipe used A alone is used for 6 hours and then it is turned off.
- Pipe B finish filling in 18 hours (after pipe A is turned off).
By definition, these formulas can be used for Work-Rate problems:
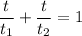

Where:
- This is the individual time for the first object:
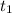
-This is the individual time for the second object:
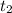
- And "t" is the time for both objects together.
In this case, having the first equation:

You can set up the second equation:
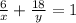
Notice that the sum of that fraction is equal to the part of the tank filled: 1 (the whole tank).
Now you can set up the System of equations:
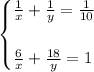
To solve it, you can apply the Elimination Method:
1. Multiply the first equation by -6.
2. Add the equations.
3. Solve for "y".
Then:
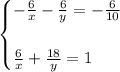
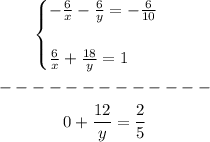
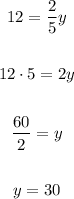
4. Substitute the value of "y" into one of the original equations.
5. Solve for "x".
Then:
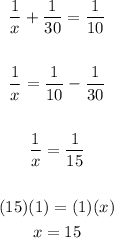
Therefore, the answer is:
- It will take pipe A 15 hours to fill the tank alone.
- It will take pipe B 30 hours to fill the tank alone.