Question

Use the ‘g’ values from #5 to compare how long it takes for an object dropped from the CN Tower (height of 553 m) to reach the ground. Also include the time it takes on Earth.

Answer 1

`t=10.62s`

Step-by-step explanation: The height of the object dropped from the tower can be modeled using the following equation:

`\begin{gathered} y(t)=y_o+v_ot-(1)/(2)gt^2\Rightarrow(1) \\ \end{gathered}`

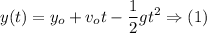
The values of the known quantities are:

`\begin{gathered} y_o=553m \\ v_o=0 \\ g=9.8ms^(-2) \\ \end{gathered}`

Setting equation (1) equal to 0 and plugging in the known values and solving for t gives the following answer:

`\begin{gathered} (553m)+(0)\cdot t-(1)/(2)(9.8ms^(-2))\cdot t^2=0 \\ \therefore\Rightarrow \\ (1)/(2)(9.8ms^(-2))\cdot t^2=(553m)\Rightarrow t^2=((553m)\cdot2)/(9.8ms^(-2))=112.86s^2 \\ t=\sqrt[]{(112.86s^2})=10.62s \\ t=10.62s \end{gathered}`

Therefore the time needed for the object to reach the ground is:

`t=10.62s`