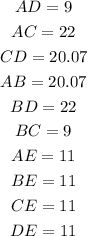Since we're working on a rectangle, we know that the diagonals intercect right in the middle, and that they're all equal.
This way,
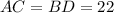
And
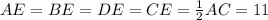
Now, we also know that
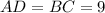
And using the Pythagorean theorem, we have that:
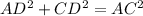
Solving for CD,
![\begin{gathered} CD=\sqrt[]{AC^2-AD^2} \\ \rightarrow CD=20.07 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zf4t8i9jjk9epccgk91m186mttubnamwpa.png)
And we know that:
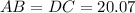
This way, the final answers would be: