Since the given line passes through the point (8, -1) and has a slope of -3/4, then
Let us use the point-slope form of the equation

Where:
m is the slope
(x1, y1) is a point on the line
Since m = -3/4
Since (x1, y1) = (8, -1)
Then
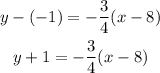
Let us simplify the right side, then put it in the form Ax + By = C
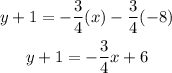
Subtract 1 from both sides
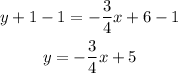
Multiply each term by 4 to cancel the denominator
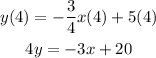
Add 3x to both sides
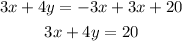
The answer is 3x + 4y = 20