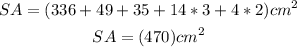Question

Please help me with the question below (also please explain).

Answer 1

336First let's calculate the surface area of the front face of the bigger prism:

`area\text{ of front face bigger prism: }12*7`

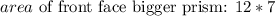
This surface area of 12*7=84, is the same area of the back face and left and right faces. Then there is 4 faces with this 84 surface area, being the total 84*4=336

Now, the base of the bigger prism is algo a surface area, wich is a square of length side 7, then the surface area of the base is 49:

`area\text{ of the base: }7*7=49`

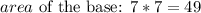
Now, the top of the figure without the smaller blue prism would be another square with 7 as the length of the side, being 7*7=49 the top surface. How ever, the top face has a smaller prism on, which is covering a part of this 49 cm^2. The part covered is 2cm*7cm, the area of the bottom face of the blue prism. Hence, the top surfaces from the bigger prism is 49-2*7=35.

Finally, the surface area from the blue small prism is the top face, with an area of 7*2=14, the right and left faces with the same 14 of area (then there is 3 faces with 14 of surface area), and the front and back faces which are squares with an area of 2*2=4 each one (then there is two faces with 4 as surface area).

The total surface area is:

`\begin{gathered} SA=(336+49+35+14*3+4*2)cm^2 \\ SA=(470)cm^2 \end{gathered}`