Question

In the rhombus, AC=24 and BD=32. Find the perimeter of the rhombus

Answer 1

Given: The diagonals of a rhombus as shown in the image

To Determine: The perimeter of the rhombus

Solution

The perimeter of a rhombus can be calculated if the diagonals are given by the formula below

`\begin{gathered} P=2√(a^2+b^2) \\ P=Perimeter \\ a=diagonal1 \\ b=diagonal2 \end{gathered}`

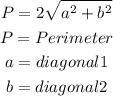
Substitute the given diagonals into the formula

`\begin{gathered} AC=24 \\ BD=32 \\ P=2√(24^2+32^2) \\ P=2√(576+1024) \\ p=2√(1600) \\ P=2*40 \\ P=80 \end{gathered}`

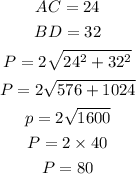
Hence, the perimeter is 80