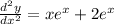Question

Let y=x*e^x. find (d^2 y/dx^2)

Answer 1

We have to find the 2nd derivative of the function:

`y=xe^x`

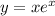
We would need to know the product rule of derivatives, which is:

If u and v are two functions, then the derivative of u*v is:

`\begin{gathered} \text{If y=uv} \\ dy=uv^(\prime)+vu^(\prime) \end{gathered}`

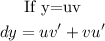
So, we have:

`(dy)/(dx)=x(d)/(dx)(e^x)+e^x(d)/(dx)(x)`

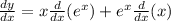
Remember, the derivative of e^x is e^x and the derivative of "x" is 1.

Thus, we have:

`\begin{gathered} (dy)/(dx)=x(d)/(dx)(e^x)+e^x(d)/(dx)(x) \\ (dy)/(dx)=xe^x+e^x(1) \\ (dy)/(dx)=xe^x+e^x \end{gathered}`

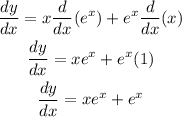
To get the 2nd derivative, we again have to use the product rule of differentiation on xe^x and just do the differentiation of e^x and sum it. Thus, the process is shown below:

`\begin{gathered} (dy)/(dx)=xe^x+e^x \\ (d^2y)/(dx^2)=x(d)/(dx)(e^x)+e^x(d)/(dx)(x)+(d)/(dx)(e^x) \\ (d^2y)/(dx^2)=xe^x+e^x+e^x \\ (d^2y)/(dx^2)=xe^x+2e^x \end{gathered}`

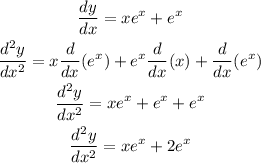
The 2nd derivative of the function shown is:

`(d^2y)/(dx^2)=xe^x+2e^x`