First, we solve each inequality for y:
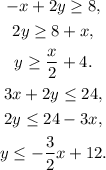
First, for -x+2y≥8 notice that all solutions (x,y) are such that y≥x/2+4, meaning that they are above the line y=x/2+4, then, the graph of the solution set of -x+2y≥8 is:
Now, for 3x+2y≤24 notice that all solutions (x,y) are such that y≤-3x/2+12, meaning that they are below the line y=-3x/2+12, then the graph of the solution set of -x+2y≥8 and 3x+2y≤24 the following intersection:
Then, we only consider the points (x,y) such that both x and y are positive numbers:
Finally, the solution set of the inequality system is:
Answer: The vertices of the solution set are (4,6), (0,12), and (0,4)