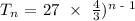ANSWER
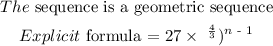
Step-by-step explanation
Given information
The given sequence is; 27, 36, 48, 64
To determine whether the given sequence is arithmetic or geometric, we will need to calculate the common difference and common ratio of the sequence.
Common difference = Next term - previous term
36 - 27 = 9
48 - 36 = 12
64 - 48 = 16
From the above calculations, you will see that the difference between the next term and the previous term is not consistent. Hence, the sequence can not be arithmetic
The next step is to determine the common ratio of the sequence
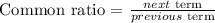
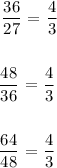
From the above calculations, you will see that the ratio of the next term to the previous term remains constant. Hence, the common ratio is 4/3. Therefore, the sequence is a geometric sequence
Part B
Find an explicit formula for the nth term of the sequence.
Since we know that the sequence is a geometric sequence, therefore, we can use the below formula to find the explicit formula
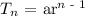
Where
a = first term of the sequence
r = common ratio of the sequence
n = number of terms
a = 27
r = 4/3
Substitute the above into the geometric sequence term
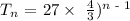
Hence, the explicit formula of the geometric sequence is