Question

A wire is stretched from the ground to the top of antenna tower. The wire is 25 feet long. The height of the tower is 5ft greater than the distance d from the tower’s base to the end of the wire. Find the distance d and the height of the tower.

Answer 1

distance = 15 ft

Height = 20 ft

Step-by-step explanation:

We can model the situation as:

Now, we can apply the Pythagorean theorem and formulate the following equation:

`25^2=d^2+(d+5)^2`

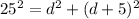
So, solving for d, we get:

`\begin{gathered} 25^2=d^2+(d^2+2\cdot d\cdot5+5^2) \\ 625=d^2+d^2+10d+25 \\ 625=2d^2+10d+25 \\ 0=2d^2+10d+25-625 \\ 0=2d^2+10d-600 \end{gathered}`

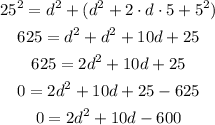
So, we can divide both sides by 2 and get:

`\begin{gathered} (2d^2)/(2)+(10d)/(2)-(600)/(2)=(0)/(2) \\ d^2+5d-300=0 \end{gathered}`

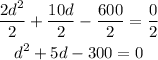
Then, we can factorize and find the solutions as:

`\begin{gathered} (d+20)(d-15)=0 \\ d+20=0 \\ d=-20 \\ or \\ d-15=0 \\ d=15 \end{gathered}`

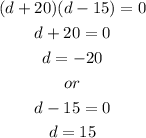
Since d=-20 have no sense in this problem, the distance d is equal to 15 ft.

So, the height of the tower is:

d + 5 = 15 + 5 = 20 ft

Therefore, the distance d is 15 ft and the height of the tower is 20 ft