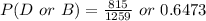Step-by-step explanation
We are given the following information from the table in the image:

We are required to determine the probability that the next fish caught is a drum or bluefish.
We can determine the probability with the following details:
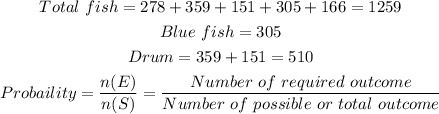
Therefore, the probability that the next fish caught is a drum or bluefish is:
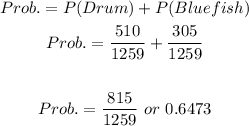
Hence, the answer is: