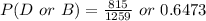Question

The type and number of fish caught in the Charleston Harbor in March was recorded for a month. The results are recorded in the table below. What is the probability that the next fish caught is a drum or bluefish? Enter a fraction or round your answer to four decimal places if necessary

Answer 1

Step-by-step explanation

We are given the following information from the table in the image:

`\begin{gathered} Flounder=278 \\ Red\text{ }drum=359 \\ Black\text{ }drum=151 \\ Blue\text{ }fish=305 \\ Sea\text{ }Trout=166 \end{gathered}`

We are required to determine the probability that the next fish caught is a drum or bluefish.

We can determine the probability with the following details:

`\begin{gathered} Total\text{ }fish=278+359+151+305+166=1259 \\ Blue\text{ }fish=305 \\ Drum=359+151=510 \\ Probaility=(n(E))/(n(S))=\frac{Number\text{ }of\text{ }required\text{ }outcome}{Number\text{ }of\text{ }possible\text{ }or\text{ }total\text{ }outcome} \end{gathered}`

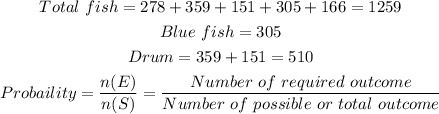
Therefore, the probability that the next fish caught is a drum or bluefish is:

`\begin{gathered} Prob.=P(Drum)+P(Bluefish) \\ Prob.=(510)/(1259)+(305)/(1259) \\ \\ Prob.=(815)/(1259)\text{ }or\text{ }0.6473 \end{gathered}`

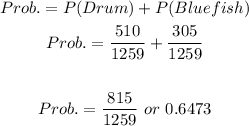
Hence, the answer is:

`P(D\text{ }or\text{ }B)=(815)/(1259)\text{ }or\text{ }0.6473`