Question

Question 10 of 10Which of these expressions can be used to calculate the monthly payment fora 30-year loan for $195,000 at 6.6% interest, compounded monthlyO A$195 000 0.0055(1 +0.0055) 300(1 +0.0055)300 + 1B.$195 000 0.0055(1 -0.0055) 60(1 -0.0055)300 - 1C.$195 000 0.0055 (13600055)RE(1 +0.0055)D$195 000 0.0055 (1 -0.0055560(1 -0.0055) 300 +1

Answer 1

`M=(\lbrack195,000\cdot(1+0.0055)^(3)^(6)^(0)\rbrack)/(360)`

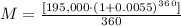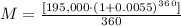
1) Let's calculate the monthly payment, considering the following about this:

`\begin{gathered} M=(\mleft[P\cdot(1+(r)/(n))\mright]^(nx))/(nx) \\ \\ M=(\mleft[195,000\cdot(1+(0.066)/(12))^(3)^(6)^(0)\mright])/(360) \\ M=\$3901.92 \end{gathered}`

Note that we call the Principal, i.e. $195,000 an interest rate of 6.6% (or 0.06%) note that there is no mention of any down payment. And the x variable stands for the duration of the loan. Also, n stands for the number of months within a year.

2) We need to do a little adjustment so that the answer might fit into the options, rewriting the fraction as a decimal number we have

2) Thus, the answer is:

`M=(\lbrack195,000\cdot(1+0.0055)^(3)^(6)^(0)\rbrack)/(360)`